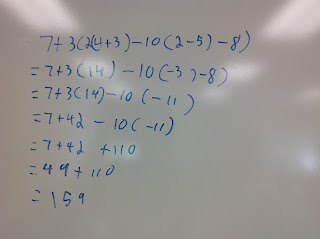I CAN do math!

Confidence is a huge part of mathematical success yet something that is so fragile. It takes only one small event to crush mathematical confidence and so much more work to regain or establish it. This often leads to less resilience in mathematics classrooms.

When I learn a new skills (anywhere but in the math classroom), I expect to make lots of mistakes and learn from them. If I'm not making mistakes, then I am not learning. I've learnt to play the piano and hitting a wrong note was not a big deal. You just played the correct note and carried on with the song. I swam competitively in high school and I didn't give up when I lost goggles on a dive in some races. Yet mistakes in the mathematics classroom often seem to mean something completely different.

Often what students in math classes think is "If I can't get it perfect on the first attempt, then I will never be able to do it" or "I have to be able to perform quickly or else I am not good at math". There is no room or time for mathematical mistakes and as soon as I make a mistake, it must mean I am not good at math.

So why am I so concerned with mathematical confidence? If I have confidence in my mathematical abilities, I will
1. be able to critically look at my work.
2. be able to look for minor arithmetic errors in my work instead of assuming I know nothing because my final answer does not match the answer at the back of the book.
3. be able to answer questions instead of questioning each step I make.
4. practice my skills and want to make mistakes in my homework so I know what part of my thinking is incorrect.
5. learn from my mistakes on a test instead of jumping to the conclusion that I can never do math after getting a low mark.
6. know when to continue practicing and when I have mastered the skill (without seeing a mark on the test).

As a teacher, I try to build student confidence in my classroom by
a) encouraging mistakes. I ask students to explain why they said their answer and then as a class we learning to correct our thinking from the mistake.
b) having conversations with students. I sit down with each student and talk through the solution to a question. I ask a lot "why is that _____" for both correct and incorrect answers so that students don't just assume when I question them they are incorrect. They start to justify all their answers with confidence.
c) letting students investigate ideas and collaborate. Instead of lecturing to students and simply giving them all the information that they need, I attempt to have them develop the idea in groups or as a class building on concepts that they attained in previous courses or units.

Order Really does matter

This week, we were wrapping up the first unit on Numeracy in Grade 9 and I asked the class this question: 7 + 3 (2 (4 +3) - 10(2 - 5) - 8). I wanted to ensure students followed proper BEDMAS and did not add the 7+3 before evaluating the brackets.

I posted the question on the board and asked each student to answer it individually. As I walked around the room, I noticed that every student had a different answer. So I put them into groups of three and asked them to go up to the board and solve the problem in their groups (without referring to what they individually did on paper). Surprisingly, I got three more different answers on the board:

As they solved the problem on the board, the discussion they were having in their groups about what to do first and what proper format should be was inspiring and showed their level of understanding. They started looking around the room at other groups work and one student asked "Is there only one answer to this?"

We talked about "would it be okay to have different answers". I asked "which answer would you want to get if the answer was your prize money?" and "which answer would you want to get if this was the number of steps you had to take?". We then summarized why it is important to have a set of rules to follow. It's not just a set of rules that your teacher is imposing on you, but absolutely required so that the correct answer (and unique answer) can be determined.

So what I had intended to do as a review of the unit ended up being a pretty rich conversation around order of operations and the real life need for them. 

Talking about Math

Last week, I sat down with each of my grade 12 students individually and had a mathematical conversation with them. For some students, it was the first time they had to talk math and not just do math on paper.  It was also an opportunity for them to explain their knowledge and not simply regurgitate what they memorized from a textbook.

We are currently studying polynomial functions. I started the conversation by showing students a graph of a polynomial like this (I had 20 graphs to pull from so very few students saw the same graph)

Students were asked to identify if the polynomial in the graph had an even or odd degree; the sign of the leading coefficient; the x-intercepts and their order; the least possible degree of the polynomial; and the maxima and minima of the polynomial (and identify them as local or global). Following this, students were asked a deeper thinking question based on the unit. One example was “Could a polynomial have a degree of 9 and only have 4 x-intercepts?”

Many students were very nervous (a few of them actually said “I need a minute, I am so nervous”) as the conversation was marked as part of their assessment on the characteristics of polynomial functions. However, there was no time limit on their responses and they were given thinking time before they had to answer. It was illuminating to be able to more accurately see their understanding. Too often in math, at least in my career thus far and my experience as a student, many assessments are paper test and the mark is based on what the teacher sees on paper. There is no opportunity to make corrections or clarify your response – it’s a one-chance deal. As a teacher, I try to get students to show their thought-process by having them show their steps but when they make a mistake, I am left making assumptions of why they made the mistake. With conversations, I had the opportunity to ask a student to clarify their answer and not simply attempt to decipher what they really knew based on what they wrote on the test.  Furthermore, when I asked a clarifying question, many students were able to correct mistakes without being explicitly told they were incorrect.

I look forward to the next round of conversations in our next unit!